# 回溯
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。
用回溯算法解决问题的一般步骤:
针对所给问题,定义问题的解空间,它至少包含问题的一个(最优)解。
确定易于搜索的解空间结构,使得能用回溯法方便地搜索整个解空间
以深度优先的方式搜索解空间,并且在搜索过程中用剪枝函数避免无效搜索
# 解题思路
做回溯的题,首先要尽量把目标抽象成树,把解题过程转换成如果遍历这个树的过程
如对于例子 [1,2,3] ,可以先抽象成以下结构的树,之后再根据具体题意进行解题
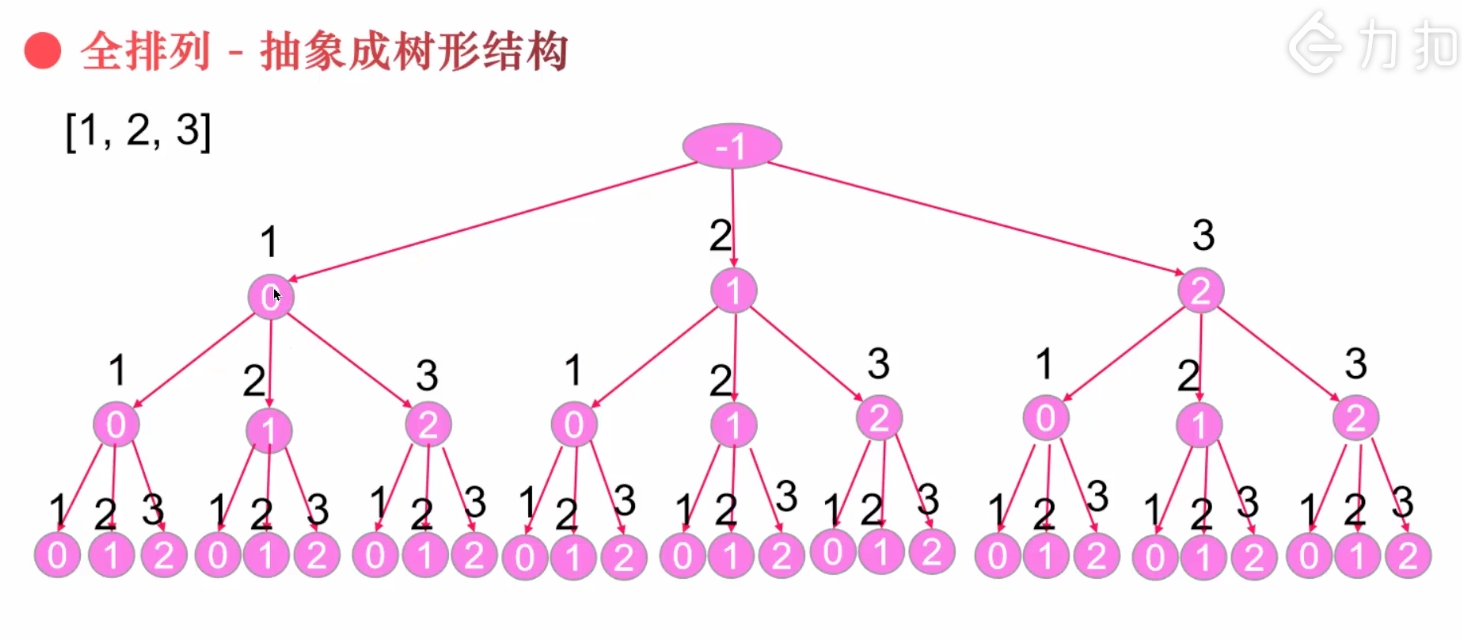
回溯是经过修改的深度优先查找方法,过程包括:对一个状态空间树进行深度优先查找,检查每个节点是否满足条件。如果不满足就回溯到该节点的父节点。算法框架(伪代码)如下:
result = []
backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
# 46. 全排列 (opens new window)
给定一个 没有重复 数字的序列,返回其所有可能的全排列
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
思路
以上面的树为例,这个题目就可以转换成,深度且前序遍历该树
如果只是使用深度且前序遍历该树的话,代码如下
var permute1 = function(nums) {
let tem = []
let walk = (n) => {
if(n === 3){ // 结果条件:到达最后一个节点结束
return
}
for(let i = 0; i<nums.length;i++){
tem.push(nums[i]) // 前序遍历,所以先保存值
walk(n+1) // 深度优先,所以递归访问下一个
}
}
walk(0)
return tem
};
根据题意做些代码改动
/**
* @param {number[]} nums
* @return {number[][]}
*/
var permute = function(nums) {
let result = [] // 遍历完一条路径后,保存这个路径
let tem = []
let len = nums.length
let walk = (n) => {
if(n === nums.length){ // 结果条件:最后一节点已经结果,出结果
result.push([...tem])
return
}
for(let i = 0; i<nums.length;i++){
if(tem.indexOf(nums[i])>-1){ // 一次路径中,如果之前已经存在该值,直接跳过
continue
}
tem.push(nums[i]) // 前序遍历,所以先保存值
walk() // 深度优先,所以递归访问下一个
tem.pop() // 回溯,移出最后一个值,表示回到上一层节点
}
}
walk()
return result
};
# 47. 全排列 II (opens new window)
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
思路
跟上一题不同之处在于现在的
nums存在重复的数,在上一题中我们是使用tem.indexOf(nums[i])>-1来判断当前这个数是否没有用过,这一题就用不了了,所以得得改用判断当前索引是否有过,这里使用哈希结构来保存当前值的索引是否有用过/** * @param {number[]} nums * @return {number[][]} */ var permuteUnique = function(nums) { let result = [] let tem = [] let map = [] nums.sort((a, b) => a - b); let walk = (n) => { if(n === nums.length){ result.push([...tem]) return } for(let i = 0; i<nums.length;i++){ if(map[i]) continue; // 根据索引来判断当前这个数是否有用过 map[i] = true // 标志当前用过的索引 tem.push(nums[i]) walk(n+1) tem.pop() map[i] = false // 还原当前用过的索引 } } walk(0) return result }; // permuteUnique([1,1,2]) 输出 [[1,1,2],[1,2,1],[1,1,2],[1,2,1],[2,1,1],[2,1,1]]上面解决了数只用一次,但是结果还是会出现重新的队列
/**
* @param {number[]} nums
* @return {number[][]}
*/
var permuteUnique = function(nums) {
let result = []
let tem = []
let map = []
nums.sort((a, b) => a - b);
let walk = (n) => {
if(n === nums.length){
result.push([...tem])
return
}
for(let i = 0; i<nums.length;i++){
// 这里有点难理解。。。
if((nums[i] === nums[i - 1] && map[i - 1]) || map[i]) continue;
map[i] = true
tem.push(nums[i])
walk(n+1)
tem.pop()
map[i] = false
}
}
walk(0)
return result
};
通过例子 [1,1,2] 来理解 nums[i] === nums[i - 1] && map[i - 1]) 的意思,首先对应的索引为 [0,1,2]
对于索引 [0,1,2] 和 [1,0,2] 都是表示值 [1,1,2]
nums[i] === nums[i - 1] && map[i - 1]) 这一判断条件则是过滤过 [0,1,2],总是最后一个满足 [1,2,3]的索引组合即 [1,0,2]
# 78. 子集 (opens new window)
/**
* @param {number[]} nums
* @return {number[][]}
*/
var subsets = function(nums) {
let path = [], res = [];
let backTrace = (start) => {
if(path.length > nums.length) return;
res.push(path.slice()); // 遍历一次就添加一个子集
for (let i = start; i < nums.length; i++) {
path.push(nums[i]);
backTrace(i + 1);
path.pop()
}
}
backTrace(0);
return res;
};
# 90. 子集 II (opens new window)
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2]
输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
题解
/**
* @param {number[]} nums
* @return {number[][]}
*/
var subsetsWithDup = function(nums) {
let result = [], tem = []
let walk = (start) => {
if(start > nums.length){
return
}
result.push([...tem])
for(let i = start; i<nums.length;i++){
if(i>start&&nums[i-1]===nums[i]){
continue
}
tem.push(nums[i])
walk(i+1)
tem.pop()
}
}
walk(0)
return result
};
重点再于 if(i>start&&nums[i-1]===nums[i])
考虑数组 [1,2,2],选择下标0 1 和 0,2都会得到相同的子集。
也就是说,对于当前选择的数 x,若前面有与其相同的数 y,放弃其中一个的继续遍历
我们可以通过判断这种情况,来避免生成重复的子集。代码实现时,可以先将数组排序;迭代时,若发现没有选择上一个数,且当前数字与上一个数相同,则可以跳过当前生成的子集
https://juejin.cn/post/6887049646988853262#heading-4
https://zhuanlan.zhihu.com/p/54275352