# 简单排序
捋捋基本排序算法
# 选择排序
思路:
第一次循环,第一个位置开始,找出最小元素的位置,然后与第一个位置进行交换
第二次循环,第二个位置开始,在剩余的元素中打出最小元素的元素,然后与第二个位置进行交换
以此类推,遍历到倒数第二个元素
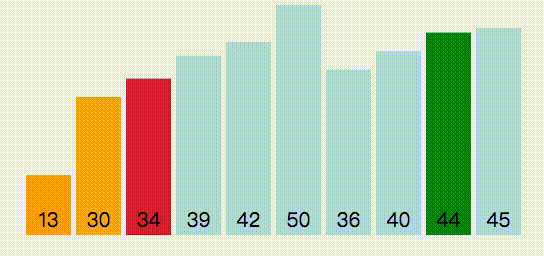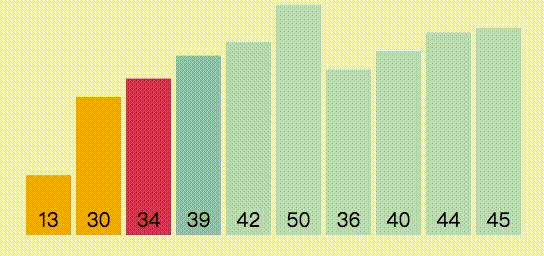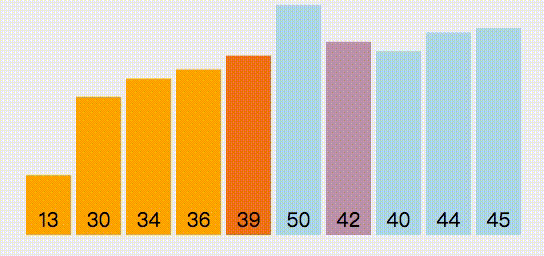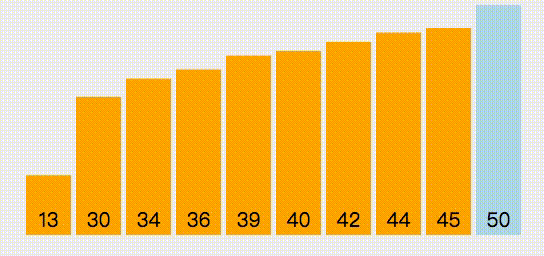
let count = 0;
const arr = [1, 20, 10, 30, 22, 11, 55, 24, 31, 88, 12, 40, 50];
let a = 0
for(let i = 0; i< arr.length - 1; i++) {
a = i
for(let j = i+1; j<arr.length; j ++) {
if(arr[j] < arr[a]) {
a = j
}
count++
}
const tem = arr[i]
arr[i] = arr[a]
arr[a] = tem
}
console.log('resultArr', arr, count)
// [1, 10, 11, 12, 20, 22, 24, 30, 31, 40, 50, 55, 88] 78
复杂度
时间复杂度:平均时间复杂度是O(n^2),这是一个不稳定的算法,因为每次交换之后,它都改变了后续数组的顺序。
空间复杂度:辅助空间是常数,空间复杂度为O(1);
# 快速排序
思路:
选择一个数作为参照数,遍历剩余数据,比参数照小的放在参照数的左边,反之后在右边。
然后用同样的方式递归那两个分出来的数据,直接分出来的数组数量为1时,停止循环

let count = 0;
const data = [1, 20, 10, 30, 22, 11, 55, 24, 31, 88, 12, 40, 50];
function quickSort(arr) {
if(arr.length <= 1) {
return arr
}
const flag = arr[0]
const left = []
const right = []
for(let i = 1; i< arr.length; i++) {
if(arr[i] > flag) {
right.push(arr[i])
} else {
left.push(arr[i])
}
count += 1
}
return quickSort(left).concat([flag], quickSort(right))
}
const result = quickSort(data)
console.log('resultArr', result, count)
// [1, 10, 11, 12, 20, 22, 24, 30, 31, 40, 50, 55, 88] 41
复杂度
时间复杂度:平均时间复杂度O(nlogn),只有在特殊情况下会是O(n^2),不过这种情况非常少
空间复杂度:辅助空间是logn,所以空间复杂度为O(logn)
# 冒泡排序
思路: 从第一个元素开始与下一个元素相比较,如果大于下一个元素,则交换两个元素的位置。如此步骤循环整个元素
let count = 0
const arr = [1, 20, 10, 30, 22, 11, 55, 24, 31, 88, 12, 40, 50]
for(let i = 0; i< arr.length - 1; i++) {
for(let j = 0; j<arr.length - 1 - i; j ++) {
if(arr[j] > arr[j+1]) {
const temp = arr[j]
arr[j] = arr[j+1]
arr[j+1] = temp
}
count++
}
}
console.log('resultArr', arr, count)
// [1, 10, 11, 12, 20, 22, 24, 30, 31, 40, 50, 55, 88] 78
使得冒泡排序,共循环了78次
复杂度
时间复杂度:平均时间复杂度是O(n^2)
空间复杂度:由于辅助空间为常数,所以空间复杂度是O(1)
# 优化一
以上代码有个缺点就是,无论是排序的数组原来的数据是乱序还是正序,都会执行78次才能结束, 但实际上,只要有某一次的循环未进行数据交换,那么这组数据其实已经是正序的状态,我们就可以结束排序了
let count = 0;
const arr = [1, 20, 10, 30, 22, 11, 55, 24, 31, 88, 12, 40, 50]
for(let i = 0; i< arr.length - 1; i++) {
let flag = false
for(let j = 0; j<arr.length - 1 - i; j ++) {
if(arr[j] > arr[j+1]) {
const temp = arr[j]
arr[j] = arr[j+1]
arr[j+1] = temp
flag = true
}
count++
}
if(!flag) {
break
}
}
console.log('resultArr', arr, count)
// [1, 10, 11, 12, 20, 22, 24, 30, 31, 40, 50, 55, 88] 68
循环次数减少了10次,如果本来就是正序的话,循环次数就只有数组的个数
# 优化二
记录最后一次交换的位置,因为之后的数都是可以不用排序的,可以不遍历这些数
let count = 0;
let last = arr.length
for(let i = last - 1; i >= 0; i--) {
let flag = true;
for(let j =0; j<i; j++) {
if(arr[j] > arr[j+1]) {
const tem = arr[j]
arr[j] = arr[j+1]
arr[j+1] = tem
last = j + 1
flag = false
}
count += 1
}
if(flag) {
break
}
}
console.log('arr', arr, count)
// [1, 10, 11, 20, 12, 22, 24, 30, 31, 40, 50, 55, 88] 57
# 插入排序
第一次遍历,取第二个元素,那么第1个元素就是已经排好的数组,将这个元素插入到已排好的数组中
第二次遍历,取第三个元素,那么第1个元素到第二个元素就是已经排好的数组,将这个元素插入到已排好的数组中
以此类推,直到最后一个元素插入完成
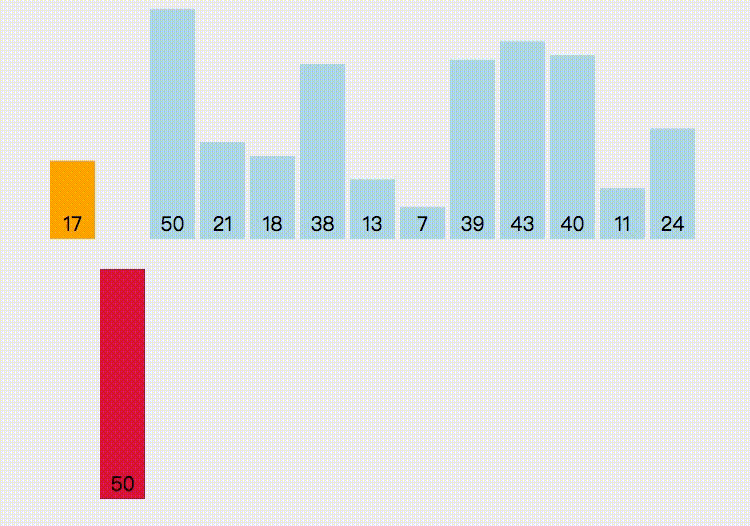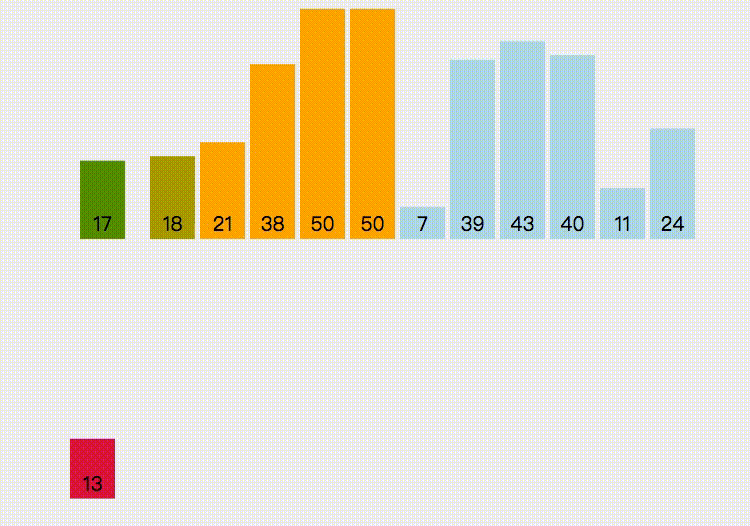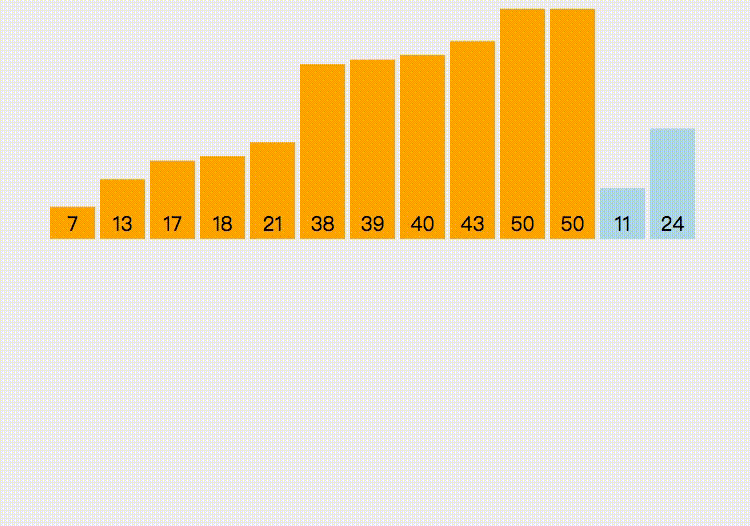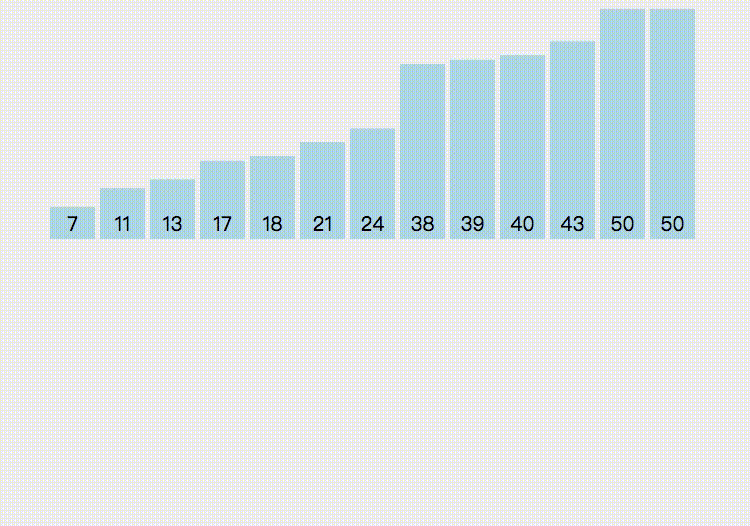
const arr = [1, 20, 10, 30, 22, 11, 55, 24, 31, 88, 12, 40, 50];
let count = 0;
for(let i = 0; i < arr.length; i++) {
let temp = arr[i];
for (let j = 0; j < i; j++) {
count += 1
if (temp < arr[j] && j === 0) {
arr.splice(i, 1);
arr.unshift(temp);
break;
} else if (temp > arr[j] && temp < arr[j + 1] && j < i - 1) {
arr.splice(i, 1);
arr.splice(j + 1, 0, temp);
break;
}
}
}
console.log('arr', arr, count)
// [1, 10, 11, 12, 20, 22, 24, 30, 31, 40, 50, 55, 88] 59
复杂度
时间复杂度:平均算法复杂度为O(n^2)
空间复杂度:辅助空间为常数,空间复杂度是O(1)
# 归并排序
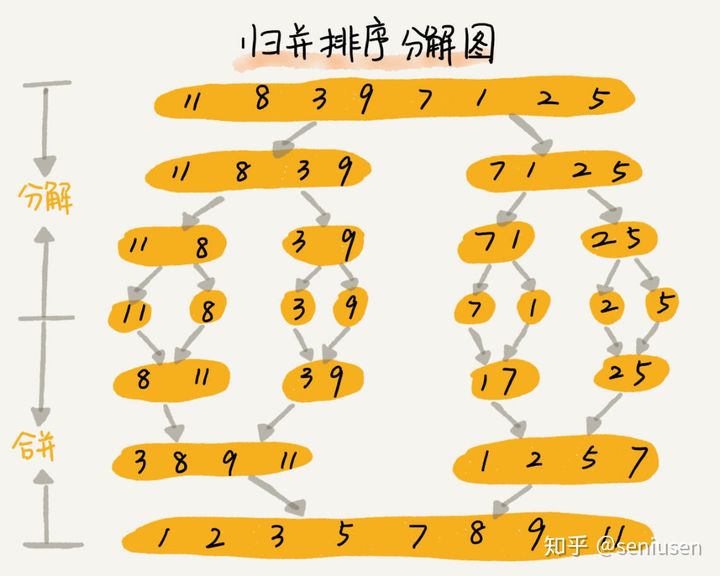
思路:
将数组从中间切分为两个数组
切分到最小之后,开始归并操作,即合并两个已排序的数组
递归合并的过程,由于是从小到大合并,所以待合并的两个数组总是已排序的,一直做同样的归并操作就可以
function mergeSort(unsorted) {
function merge(leftArr, rightArr) {
const lenL = leftArr.length;
const lenR = rightArr.length;
let indexL = 0;
let indexR = 0;
const result = [];
while (indexL < lenL && indexR < lenR) {
if (leftArr[indexL] < rightArr[indexR]) {
result.push(leftArr[indexL++]);
} else {
result.push(rightArr[indexR++]);
}
}
while (indexL < lenL) {
result.push(leftArr[indexL++]);
}
while (indexR < lenR) {
result.push(rightArr[indexR++]);
}
return result;
}
function split(array) {
const len = array.length;
if (len <= 1) {
return array;
}
const mid = Math.floor(len / 2);
const leftArr = array.slice(0, mid);
const rightArr = array.slice(mid, len);
return merge( split(leftArr), split(rightArr) );
}
return split(unsorted);
}
show(mergeSort);
// ------------------------------------------
// Method: mergeSort
// ------------------------------------------
// before:
// 86,55,0,31,104,6,5,49,89,19,6
// after:
// 0,5,6,6,19,31,49,55,86,89,104
复杂度
选择排序和冒泡排序的时间复杂度都是 O(n^2),很少用在实际工程中;归并排序的时间复杂度是 O(nlog(n)),是实际工程中可选的排序方案
# Array.sort
Array.sort (opens new window) 会将元素类型转换成字符串Unicode码点进行排序。不过他是一个高阶函数,可以接受一个函数做为参数。我们可以通过这函数,来调整数组的升序或降序
Array.sort 有一个特点就是默认按字符串排序,粟子:
const arr = [1, 20, 10, 30, 22, 11, 55, 24, 31, 88, 12, 100, 50]
arr.sort(); // [1, 10, 100, 11, 12, 20, 22, 24, 30, 31, 50, 55, 88]
从上面的结果可以看到因为默认是按字符串排序,所以排出来的结果有问题的
带函数参数排序
Array.sort 可以接收一个函数参数,sort 将根据这个参数函数的返回值(return)进行排序,以 compareFunction(a, b) 为例:
如果
return小于 0 ,那么 a 会被排列到 b 之前如果
return大于 0 ,那么 a 会被排列到 b 之后如果
return等于 0 , a 和 b 的位置不变
var arr = [1, 20, 10, 30, 22, 11, 55, 24, 31, 88, 12, 100, 50];
arr.sort(function(a, b){
return -(a - b)
})
// [1, 10, 11, 12, 20, 22, 24, 30, 31, 50, 55, 88, 100]
上面只适用于全是数字的数组,如果数组元素包含字符串就不行了
'a' - 'b' // NaN
含有字符串数组的处理
字符串是不能相减但是可以比较大小
var arr = ['wanna', 'take', 'it', 'back', 'and', 'start', 'again'];
arr.sort(function(a, b){
return a < b ? -1 : 1
})
// ["again", "and", "back", "it", "start", "take", "wanna"]
如果是对象元素,可以使用属性进行排序
var items = [
{ name: 'Edward', value: 21 },
{ name: 'Sharpe', value: 37 },
{ name: 'And', value: 45 },
{ name: 'The', value: -12 },
{ name: 'Magnetic' },
{ name: 'Zeros', value: 37 }
];
// sort by value
items.sort(function (a, b) {
return (a.value - b.value)
});
// sort by name
items.sort(function(a, b) {
var nameA = a.name.toUpperCase(); // ignore upper and lowercase
var nameB = b.name.toUpperCase(); // ignore upper and lowercase
if (nameA < nameB) {
return -1;
}
if (nameA > nameB) {
return 1;
}
// names must be equal
return 0;
});