# 字节前端算法题
# 合并两个有序数组(简单) (opens new window)
给你两个有序整数数组 nums1 和 nums2,请你将 nums2 合并到 nums1 中,使 nums1 成为一个有序数组。
初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。你可以假设 nums1 的空间大小等于 m + n,这样它就有足够的空间保存来自 nums2 的元素。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
提示:
- nums1.length == m + n
- nums2.length == n
- 0 <= m, n <= 200
- 1 <= m + n <= 200
- -109 <= nums1[i], nums2[i] <= 109
思路:
创建两个指针,一个从
num1开始,一个从num2开始,判断两个指针指向的值的大小,进行交换
但是要注意不从前往后开始遍历,因为如果从前往后遍历的话,在交换位置,还需要考虑被交换的元素与其它元素的大小于情况
所以需要从后往前遍历,将满足的元素直接从后往前插入,将可以一步到位
/**
* @param {number[]} nums1
* @param {number} m
* @param {number[]} nums2
* @param {number} n
* @return {void} Do not return anything, modify nums1 in-place instead.
*/
var merge = function(nums1, m, nums2, n) {
let start1 = m-1, start2 = n - 1
let total = m+n-1
while(start1 >= 0 && start2 >= 0){
if(nums1[start1] <= nums2[start2]){
nums1[total] = nums2[start2]
start2--
} else {
nums1[total] = nums1[start1]
start1--
}
total--
}
while(start2 >= 0){
nums1[start2] = nums2[start2]
start2--
}
return nums1
};
# 长度最小的子数组(中等) (opens new window)
给定一个含有 n个正整数的数组和一个正整数 target
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
思路:
创建
start,end两个指针,分别指向最开始的位置计算
start和end之间的和不满足条件时,则保持
start不动,end不断右移,直到和满足条件为止当上一步满足条件时,尝试移除最左侧的元素,看剩下的元素加起来是否也条件
1,2,3,4 的和大于 7 但此时 2,3,4 和 3,4也是可以大于7的
/**
* @param {number} target
* @param {number[]} nums
* @return {number}
*/
var minSubArrayLen = function(target, nums) {
let result = 0 // 结果
let len = nums.length
let start = 0, end = 0
let count = nums[0]
while(end <= nums.length){
if(count >= target){
result = result ? Math.min(result, end-start+1): end-start+1
if(result === 1) break // 如果没1,最小值长度了,直接返回
count -= nums[start] // 长度大于1时, 减掉最左边的值,看下是否还能满足条件
start++ // 右移 start 指针
continue // 直接进入判断当前count是否满足值
}
end ++
count += nums[end]
}
return result
};
# 路径总和(简单) (opens new window)
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ,判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和targetSum
叶子节点 是指没有子节点的节点。
示例:
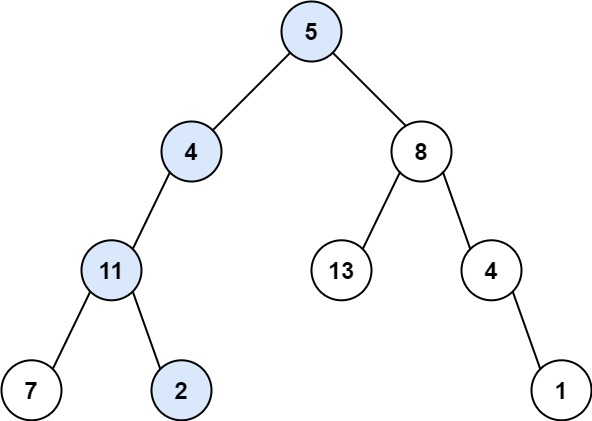
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解一:使用深度优先遍历的方式计算每个分支的合,可以使用递归
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} targetSum
* @return {boolean}
*/
var hasPathSum = function(root, targetSum) {
if(root === null) return false
if(!root.left && !root.right && root.val === targetSum) return true // 如果没有节点,且满足条件了则直接返回
return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val) // 递归调用
};
解一:使用广度优先遍历的方式
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} targetSum
* @return {boolean}
*/
var hasPathSum = function(root, targetSum) {
let stack = [root]
while(stack.length){
let cur = stack.shift()
if(!cur) continue
if(!cur.left&&!cur.right&&cur.val === targetSum) {
return true
}
if(cur.left){
cur.left.val += cur.val // 添加上一节点的值
}
stack.push(cur.left)
if(cur.right){
cur.right.val += cur.val // 添加上一节点的值
}
stack.push(cur.right)
}
return false
};
# 数组中的第K个最大元素(中等) (opens new window)
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
说明:
你可以假设 k 总是有效的,且 1 ≤ k ≤ 数组的长度。
解法一:
排序后,直接取 k 位置
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var findKthLargest = function(nums, k) {
let arr = nums.sort((a,b) => a>=b ? -1:1)
return arr[k-1]
};
解法二:
其实不是全部排序后才能得到 K 位置,只在 K 位置之前是排好序就可以了
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var findKthLargest = function(nums, k) {
if(nums.length < k) {
return
}
if(nums.length === k) {
return findMin(nums)
}
let mid = nums[0]
let left = []
let right = []
for(let i=1; i<nums.length; i++){
if(nums[i] <= mid){
left.push(nums[i])
} else if(nums[i] > mid) {
right.push(nums[i])
}
}
if(right.length === k-1){
return mid
}
else if(right.length >= k){
return findKthLargest(right, k)
} else {
return findKthLargest(left, k-right.length-1)
}
};
function findMin(nums){
let min = nums[0]
for(let i of nums){
min = Math.min(min, i)
}
return min
}
# 字符串相加 (opens new window)
给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和
提示:
num1 和num2 的长度都小于 5100
num1 和num2 都只包含数字0-9
num1 和num2 都不包含任何前导零
你不能使用任何內建 BigInteger 库,也不能直接将输入的字符串转换为整数形式
题解:模块加法运算
/**
* @param {string} num1
* @param {string} num2
* @return {string}
*/
var addStrings = function(num1, num2) {
let start = 1
let result = ''
let add = 0
while((num1.length - start) > -1 || (num2.length -start) > -1){
let n1 = num1[num1.length - start] || 0
let n2 = num2[num2.length - start] || 0
let count = +n1 + +n2 + add
result = count%10 + result
add = count/10 | 0
start++
}
if(add > 0){
result = add + result
}
return result
};
# 翻转二叉树 (opens new window)
翻转一棵二叉树
示例:
输入:
4
/ \
2 7
/ \ / \
1 3 6 9
输出:
4
/ \
7 2
/ \ / \
9 6 3 1
解法一:使用递归
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {TreeNode}
*/
var invertTree = function(root) {
if(!root) return null
let tem = invertTree(root.right)
root.right = invertTree(root.left)
root.left = tem
return root
};
解法二:迭代法,利用每个节点都引用类型的特性
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {TreeNode}
*/
var invertTree = function(root) {
if(!root) return root
let stack = [swap(root)]
while(stack.length){
let node = stack.shift()
node.left&&stack.push(swap(node.left))
node.right&&stack.push(swap(node.right))
}
function swap(node){
let tem = node.left
node.left = node.right
node.right = tem
return node
}
return root
};
# 求根到叶子节点数字之和 (opens new window)
给定一个二叉树,它的每个结点都存放一个 0-9 的数字,每条从根到叶子节点的路径都代表一个数字。
例如,从根到叶子节点路径 1->2->3 代表数字 123。
计算从根到叶子节点生成的所有数字之和。
说明: 叶子节点是指没有子节点的节点。
示例 1:
输入: [1,2,3]
1
/ \
2 3
输出: 25
解释:
从根到叶子节点路径 1->2 代表数字 12.
从根到叶子节点路径 1->3 代表数字 13.
因此,数字总和 = 12 + 13 = 25.
示例 2:
输入: [4,9,0,5,1]
4
/ \
9 0
/ \
5 1
输出: 1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495.
从根到叶子节点路径 4->9->1 代表数字 491.
从根到叶子节点路径 4->0 代表数字 40.
因此,数字总和 = 495 + 491 + 40 = 1026.
解法一:深度优先遍历
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var sumNumbers = function(root) {
let result = 0
var sum = function(node, count){
let s = count * 10 + node.val
if(!node.left && !node.right){
result = result + s
} else {
node.left&&sum(node.left, s)
node.right&&sum(node.right, s)
}
}
sum(root, 0)
return result
};
解法二:深度优先遍历
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var sumNumbers = function(root) {
let result = 0
let stack = [root]
while(stack.length){
let node = stack.shift()
if(!node.left && !node.right){
result += node.val
continue
}
if(node.left){
node.left.val += node.val*10
stack.push(node.left)
}
if(node.right){
node.right.val += node.val*10
stack.push(node.right)
}
}
return result
};
# 路径总和 II (opens new window)
给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
说明: 叶子节点是指没有子节点的节点。
示例: 给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
返回:
[
[5,4,11,2],
[5,8,4,5]
]
题解:
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} targetSum
* @return {number[][]}
*/
var pathSum = function(root, targetSum) {
if(!root) return []
let result = []
var wakl = function(node, count, stack){
stack.push(node.val)
count += node.val
if(!node.left&&!node.right&&count === targetSum){
result.push(stack]
}
if(node.left){
wakl(node.left, count, [...stack])
}
if(node.right){
wakl(node.right, count, [...stack])
}
}
wakl(root, 0, [])
return result
};
上面代码最主要的问题在于递归 wakl 方法时,总是要复制一次数组,这一步造成了额外的空间消耗。所以使用回逆方法做下优化
var pathSum = function(root, targetSum) {
if(!root) return []
let result = []
var wakl = function(node, count, stack){
stack.push(node.val)
count += node.val
if(!node.left&&!node.right&&count === targetSum){
result.push(stack.slice()) // 复制结果,这样不受下面 `pop()` 的影响
}
if(node.left){
wakl(node.left, count, stack)
}
if(node.right){
wakl(node.right, count, stack)
}
stack.pop() // 回逆
}
wakl(root, 0, [])
return result
};
# 两数之和 (opens new window)
解法一
遍历多次,略
解法二:两遍哈希表
使用 map 结构可以更有效的方法来检查数组中是否存在目标元素
var twoSum = function(nums, target) {
const map = {}
for(let i in nums) {
map[nums[i]] = i
}
for(let i = nums.length-1; i >=0 ; i--){
let tar = target - nums[i]
if(tar in map && map[tar] !==i ){
return [i, map[tar]]
}
}
};
方法三:一遍哈希表
方法二的优化,将两次遍历完合成一次遍历
/**
* @param {number[]} nums
* @param {number} target
* @return {number[]}
*/
var twoSum = function(nums, target) {
const map = {}
for(let i = nums.length-1; i >=0 ; i--){
let tar = target - nums[i]
if(tar in map && map[tar] !==i ){
return [i, map[tar]]
}
map[nums[i]] = i
}
};
注意点:
for(let i = nums.length-1; i >=0 ; i--)比for(let i = 0; i < nums.length ; i++)效率高,节省nums.length的计算次数for循环比forEacth效率高下面代码额外多了
result变量,会多点用点内存var twoSum = function(nums, target) { const map = {} let result = null for(let i = nums.length-1; i >=0 ; i--){ let tar = target - nums[i] if(tar in map && map[tar] !==i ){ result = [i, map[tar]] break } map[nums[i]] = i } return result };
https://github.com/afatcoder/LeetcodeTop/blob/master/bytedance/frontend.md
https://leetcode-cn.com/explore/interview/card/bytedance/